Dinamik Programlamaya Giriş
Recursive fonksiyonlarla hiç çalıştınız mı? Hani şu birbirini sürekli nested şekilde çağıran fonksiyonlar. Mesela verilen bi sayıya kadar olan sayıları toplayan fonksiyon gibi :
const sum = (n) => {
if (n != 0)
// sum() function kendini tekrar çağırıyor
return n + sum(n-1);
else
return n;
}Ya da istenilen bir Fibonacci dizilimindeki n. elemanı veren şu fonsiyon gibi:
// 1 1 2 3 5 8 13 ...
const fib = (n) => {
if (n <= 1) return n;
return fib(n-1) + fib(n-2);
}
Recursive fonksiyonlar çok şık duruyor ama performans konusunda sıkıntıları var. Örneğin yukarıdaki fibonacci fonksiyonu n'in düşük değerlerinde çok hızlı cevap verecektir ama n'i yüksek bir değer seçtiğimizde farkedeceksiniz ki yavaşlayacak. Dilerseniz hemen bir browser konsol açıp fib(7) ile fib(50) yi deneyin.
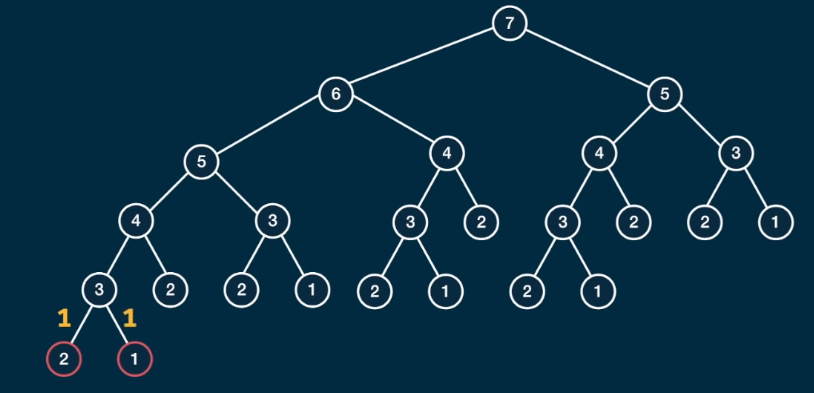
Yukarıdaki ağaç yapısını incelediğinizde n'in base değerleri (fib(1) = 1 ve fib(2) = 1) hariç, her bir dal iki farklı kırılım vermiş. Bu da fib fonksiyonunun zaman karmaşıklığını (time complexity) 2^n yapıyor. Dinamik programlama da tam burada devreye giriyor. Amacımız üssel bir zaman karmaşıklığına sahip algoritmalarımızı polinomik bir hale getirmek ve dolayısıyla performansını artırmak.
Dinamik programlamanın temelinde bir problemi, birbirini tekrar eden alt problemlere ayırmak. Alt problemlerde bir pattern yakalayıp, diğer problemlere fazla resource harcamadan erişmek temel yöntemimiz. Bunun için iki farklı metod izliyoruz: Memoization ve Tabulation.
Memoization
Hesaplanmış sonuçları cache'e atıp ve onları tekrar kullanma tekniğine verilen isimdir. Mesela aşağıda fibonacci dizininin 4.elemanını hesaplarken, gördüğünüz gibi fib(2) ve fib(3) ü iki kez hesaplamak yerine, eğer hesaplandığında bu değeri saklarsak, daha sonra ihtiyaç duyduğumuzda kullanırız. Dolayısıyla, recursive fonksiyonumuz gereksiz yere tekrar aynı değeri hesaplamaya çalışmaz.
fib(4)
fib(3)
fib(2)
fib(1)
fib(0)
fib(1) // zaten hesapladık
fib(2) // zaten hesapladıkTabulation
Bu yöntem ise aslında mantık açısından yine bir cache kullanmak olduğundan benzer bir yöntem. Buradaki yaklaşım ise cache değerlerini oluştura oluştura hedefteki sayıya ulaşmak ama bunu recursive değil de iterative şekilde yapmak. Aşağıda fibonacci problemi için yaptığımız yaklaşımı inceleyebilirsiniz. Burada bir tablo/dizi tanımladık ve n. elemana erişene kadar bu tabloyu dolduruyoruz.
mem[0] = 0
mem[1] = 1
mem[2] = mem[0] + mem[1]
mem[3] = mem[1] + mem[2]
mem[4] = mem[2] + mem[3]
mem[n] = mem[n-2] + mem[n-1]Bu yazıyı dinamik programlamaya giriş olarak kısa tutuyorum. Bir sonraki yazımla başlayarak sırasıyla en yaygın dinamik programlama problemlerini hem memoization hem de tabulation yöntemiyle çözüyor olacağız.
Aşağıya yol haritası olması açısından çözeceğimiz problemleri yazıyorum.
- Fibonacci
- CanSum
- Subset Sum Problemi
- Grid Traveller Problemi
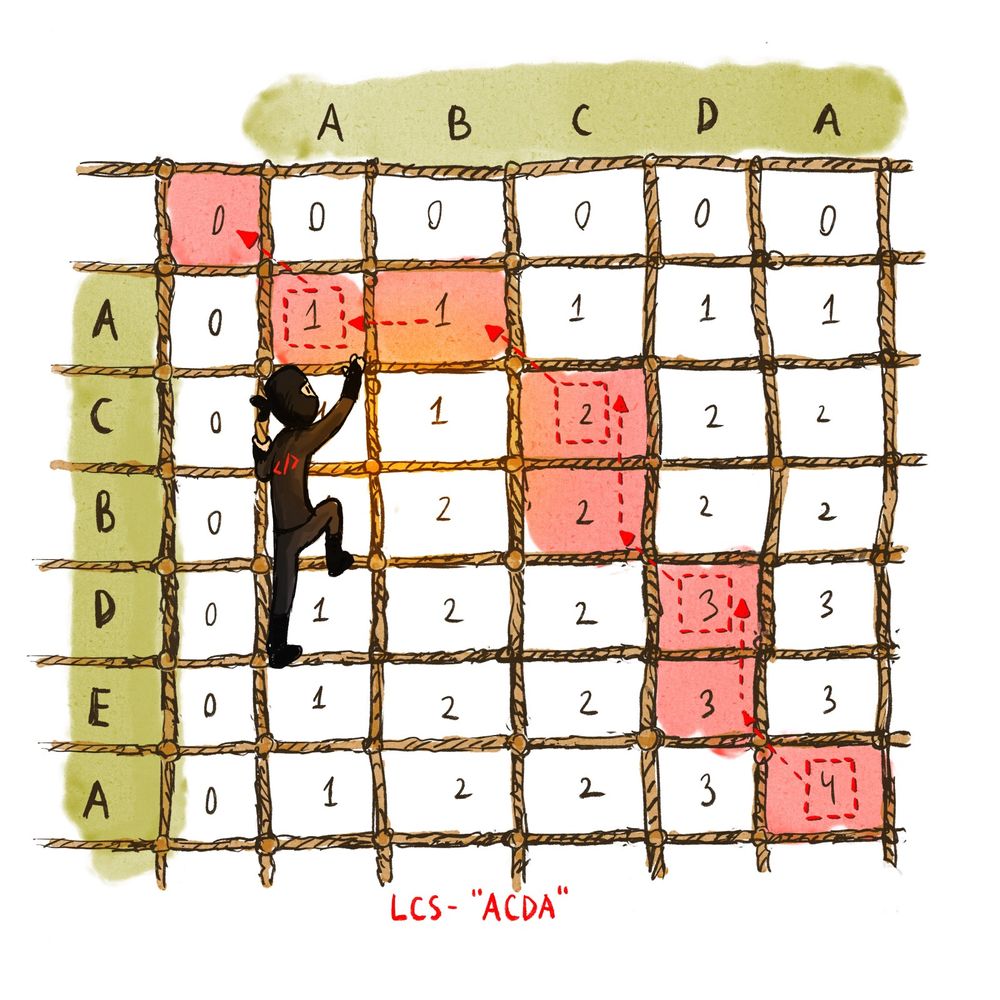
- Longest Common Subsequence Problemi
- Longest Increasing Subsequence Problemi
https://github.com/demiremrece/dynamic-programming
Not: Post thumbnaili Pramp'dan alıntıdır.