Memoization ve Tabulation #2: CanSum
Bu yazımda memoization ve tabulation yöntemlerini kullanarak canSum problemini çözeceğiz.


Memoization
Ben tarz olarak öncelikle problemi memoization kullanmadan çözüyor daha sonra metodu hızlandırmak için memoization ekliyorum. Şimdi de öyle yapıp, öncelikle problemi çözmeye odaklanalım.
Fibonacci problemini hatırlarsak, orada problemi ağaç yapısına döküp alt problemlere ayırarak çözmüştük. Aynı yaklaşımı burada da kullanacağız.
Dizinin her elamanını tekrar kullanabileceğimizden, recursive metodumuz numbers dizisini her seferinde parametre olarak alacak. Bu noktada, problemi nasıl alt problemlere ayıracağımızı düşünmemiz gerekiyor.
target => 7 numbers => [2,3]Target değerden kullanabileceğimiz elemanları çıkararak alt problemler oluşturabiliriz. Ağaç yapısında inceleyelim.
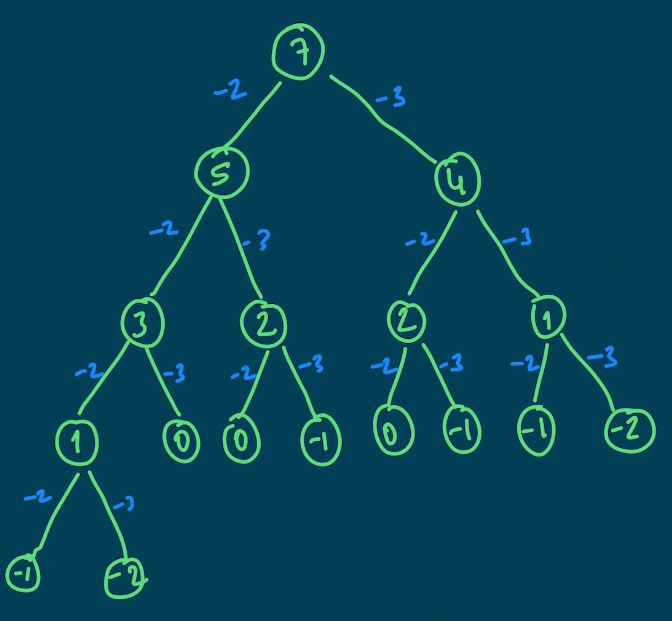
Bu şekilde alt problemlere ayırabildik. Örneğin; 7'yi elde edip edemeyeceğimizi anlamak için 5 ve 4 ü de elde edip edemeyeceğimizi bilmemiz gerekiyor. Bu şekilde elemanları kullanarak ilerleyebiliriz.
Bu noktada duracağımız yeri bilmemiz gerekiyor. Yani base caseler belirlemeliyiz. Yukarıdaki ağaç yapısına baktığımızda 2 adet base case çıkarabiliyoruz.
- 0 için true
- < 0 için false
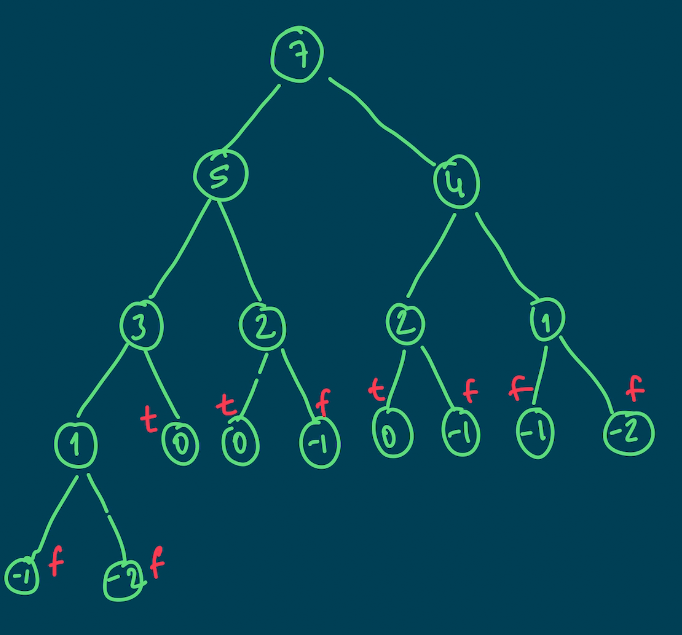
Metodumuz sadece target değeri üretip üretemeyeceğimizi sorduğu için herhangi bir true değerini gördüğümüzde problemi çözdüğümüzü varsayabiliriz. Hadi şimdi bunu koda dökelim.
const canSum = (target, numbers) => {
// Base case
if(target === 0) return true;
if (target < 0) return false;
for(let num of numbers) {
// numbers'ın her elemanını targettan çıkarıp,
// alt problemler için de metodu çağırıyoruz
const remainTarget = target - num;
// eğer hesaplayabiliyor isek, cevabımızı bulduk
if (canSum(remainTarget, numbers) === true) {
return true;
}
}
// aksi durumda false dönüyoruz.
return false;
}
console.log(canSum(7, [2,3])); // true
console.log(canSum(7, [2,4])); // false
console.log(canSum(7, [2,3,5])); // true
// Alttaki çok uzun sürecek.
// Çünkü target çok yüksek bir sayı ve kırılımları düşünürseniz, // Hesaplaması zaman alacak
console.log(canSum(300, [7,14])); // false Ağaç yapısını incelersek en kötü senaryoda target değerimizi target kere azaltabiliriz. Örneğin elemanlardan bir tanesi 1 olduğunu düşünürsek. Yani ağacın boyu en kötü senaryoda target ile eş değer olur. Metodun dallara ayrılmasındaki etken ise, direkt olarak numbers dizisinin eleman sayısı olduğunu söyleyebiliriz. Aşağıda bunu görsel olarak ifade etmeye çalıştım.
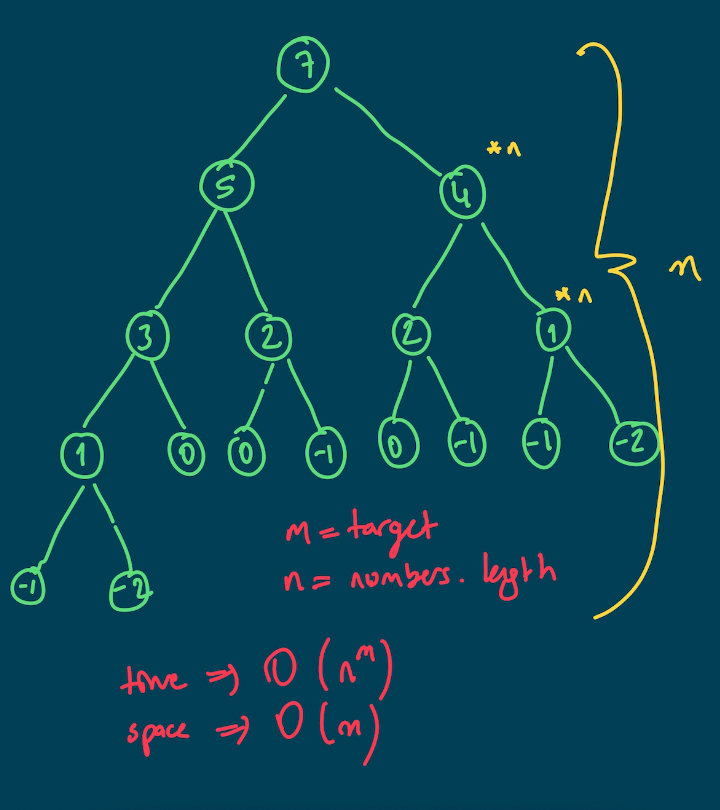
Dolayısıyla, ağacın boyu bize alan karmaşıklığımızı O(m) olarak verir. Yani maksimum m kadar canSum metodu call stack'de bulunabilir. Zaman karmaşıklığımız da bu base çözümde üssel bir değer olan O(n^m) olur. Çünkü bu kadar adet metod çağrımı yapmak zorunda kalabiliriz.
Memoization kullanarak hemen zaman karmaşıklığını azaltalım. Return değerlerimizi eğer bir memo objesinde saklarsak alt problemlerde tekrar aynı target değeri için metodumuzu çalıştırmak zorunda kalmayız.
const canSum = (target, numbers, memo = {}) => {
// Zaten hesapladıysak
if(target in memo) return memo[target];
// Base case
if(target === 0) return true;
if (target < 0) return false;
for(let num of numbers) {
// numbers'ın her elemanını targettan çıkarıp,
// alt problemler için de metodu çağırıyoruz
const remainTarget = target - num;
// eğer hesaplayabiliyor isek, cevabımızı bulduk
if (canSum(remainTarget, numbers, memo) === true) {
memo[target] = true; return true;
}
} memo[target] = false;
// aksi durumda false dönüyoruz.
return false;
}
console.log(canSum(7, [2,3])); // true
console.log(canSum(7, [5,3,4,7])); // true
console.log(canSum(7, [2,4])); // false
console.log(canSum(7, [2,3,5])); // true
console.log(canSum(300, [7,14])); // falseBu şekilde son hesaplamanın da hızlı şekilde yapılabildiğini göreceksiniz. Çünkü zaman karmaşıklığımızı Q(m*n) e indirgeyebildik. Neden? Çünkü memo objesi kullandık. Bu memo objesi en kötü senaryoda her numbers elemanı için değer cacheleyebilir. Dolayısıyla memo objesinde en fazla n kadar değer bulunabilir. Bulunan bu değerler için bir kere işlem yapıldıktan sonra tekrar aynı değer için metod çalışmayacak. Metodumuz da en kötü senaryoda m kadar çalışacağından dolayısıyla zaman karmaşıklığımız O(m*n) olur.
Tabulation
Problemimizi bu sefer tablo kullanarak iteratif şekilde çözmeye çalışalım. Tabulation yöntemiyle bir problemi çözmek istediğimizde, dikkate almamız gereken noktaları şöyle sıralayabiliriz:
- Problem bir tablo şeklinde görselleştirilmeli
- Tablonun(dizinin) boyutu girdilere göre belirlenmeli
- Tablo default(varsayılan) değerlerle ilklendirilmeli
- Tablo iteratif şekilde dolaşılıp, daha sonraki pozisyonlar bulunulan pozistyondaki değerler kullanılarak hesaplanmalı
Öncelikle problemi düşünelim. Bir target değer veriliyor ve o değere erişebilip bilmeyeceğimizi ölçmek için bir sayı dizisi. Dizimizin elemanları tekrar ve tekrar kullanılacağı için boyutu değişmeyecek. Bu yüzden bu girdiyi tablo boyutunu hesaplamak için kullanamayız. Ama target değerimizi kullanabiliriz. Memoization yönteminde de onu baz almıştık.
Örnek olarak aşağıdaki değerleri kullanalım.
target => 5 numbers => [2,3]
Bir tablo oluşturalım ve eleman sayısı target değerimizden bir fazla olsun.
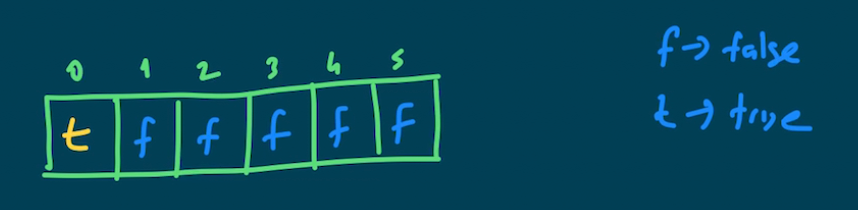
Metodumuz sonuç olarak true/false bir değer döndüreceği için tablomuzu false ile ilklendirmek hiç mantıksız değil. Tablonun her indisi alternatif hedefler olarak düşünülebilir. Örneğin; 3.indisdeki değer inputtaki elemanlar kullanarak 3 sayısını, 4. indisteki değer 4 sayısını elde edip edemeyeceğimizi göstersin. Bu koşullarda bir base case düşünmemiz lazım. Dizinin 0. indisini bu mantıkla kullanabiliriz. 0 sayısını elde verilerle elde edebildiğimizi kabul edip tablonun 0. indisini true yapalım. Sonuçta hiç bir değer kullanmadan 0 elde edebiliriz :)
Şimdi iteratif olarak sırayla her indise bakalım ve diğer pozisyonlara erişip erişemeyeceğimizi not alalım.
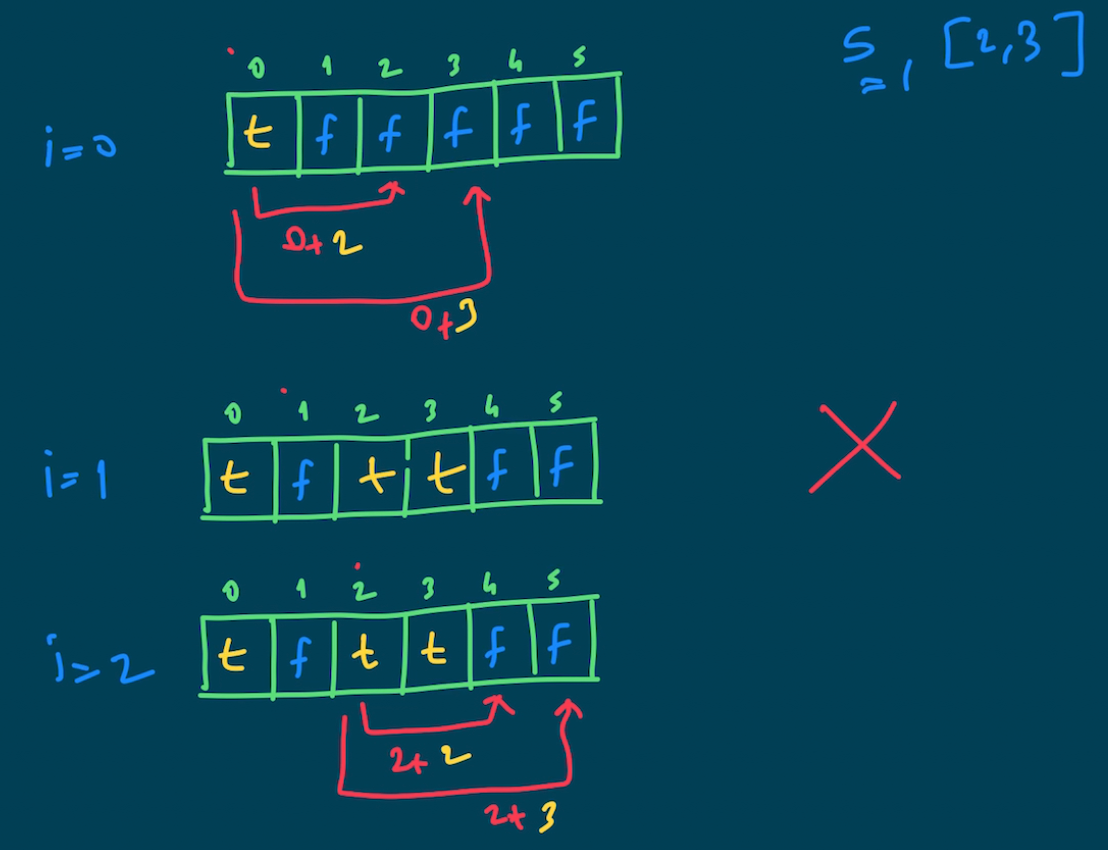
i=0 için dizideki elemanları kullanarak elde edebileceğimiz indisleri belirleyelim.
0 + 2 (kullandığımızda) = 2 elde edebiliyoruz.
0 + 3 (kullandığımızda) = 3 elde edebiliyoruz.
Dolayısıyla; table[2] = true table[3] = true
Bu şekilde i'yi bir sonraki indise kaydırarak, her eleman için tekrar ileriki pozisyonları hesaplayabiliriz. Burada dikkat etmemiz gereken nokta, eğer i'deki değeri hesaplayamıyorsak, bu pozisyonu kullanarak daha sonraki değerlere erişemeyiz demektir. Örneğin; i=1 için table[1] zaten false. Yani inputtaki değerleri kullanarak 1'i elde edemiyoruz. Elde edemeyeceğimiz değeri, diğer pozisyonları hesaplamak için kullanamayız. Algoritma kafamızda canlanmıştır diye düşünüyorum. Hadi koda geçelim...
const canSum = (targetSum, numbers) => {
// Target değerimizden bir fazla boyutlu bir dizi oluşturalım
// Dizinin her elemanını false olarak ilklendirelim
const table = Array(targetSum + 1).fill(false);
// Çözümümüz 0. elemanın elde edilebilir olduğunu varsayacaktı
table[0] = true;
// Şimdi dizi üzerinde iteratif olarak kontrol edelim
for (let i=0; i<=targetSum; i++) {
// Eğer inputla i'yi elde edebiliyorsak
if (table[i]) {
// Dizideki elemanları kullanarak diğer pozisyonları güncelleyelim
for(let num of numbers) {
// Dizi boyutundan çıkmamak için ek kontrol
// Javascript bu if kondisyonunu eklemesek de hata vermez
// Ama biz mantıklı olanı yapalım
if ((i+num) <=targetSum) {
table[i+num] = true;
}
}
}
}
// Dizinin son elemanı (targetSum indisindeki) bize sonucu verir
return table[targetSum];
}
Alan ve zaman karmaşıklığını kontrol edersek;
target => m
numbers.length => nSadece bir dizi kullanarak alan tükettiğimiz için alan karmaşıklığımız Q(m) olur. Çünkü m+1 elemanlı bir dizi oluşturuyoruz ve +1 m'in yanında göz ardı edilecek kadar küçük bir değer. Zaman karmaşıklığımızı ise iç içe 2 loop belirler. Bu yüzden zaman karmaşıklığı Q(m*n) olur.
Bir sonraki yazımda Can Sum problemini geliştirip Subset Sum problemini çözeceğiz. O problemde de verilen bir target değerini dizideki elemanları kullanarak nasıl elde edebileceğimizi bulan algoritmalar yazacağız.