Memoization ve Tabulation #1: Fibonacci

Bir önceki yazımda dinamik programlamaya bir giriş yapmıştık. Şimdi çeşitli dinamik programlama problemleriyle devam edelim. İlk olarak Fibonacci dizininde n. elemanı bulan algoritmayı hatırlayalım.

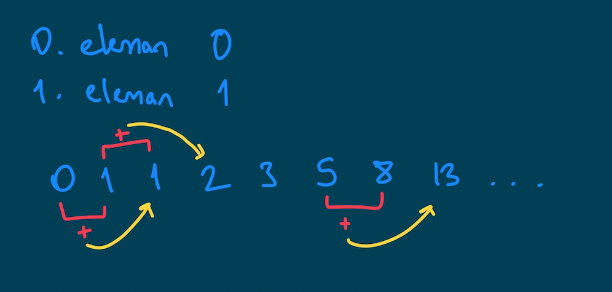
const fib = (n) => {
  if (n <= 2) return 1;

  return fib(n-1) + fib(n-2);
};

n=5 için fib metodumuzun işleyişini aşağıdaki ağaç yapısı üzerinde  kontrol ederek zaman ve alan karmaşıklığını hesaplayalım.

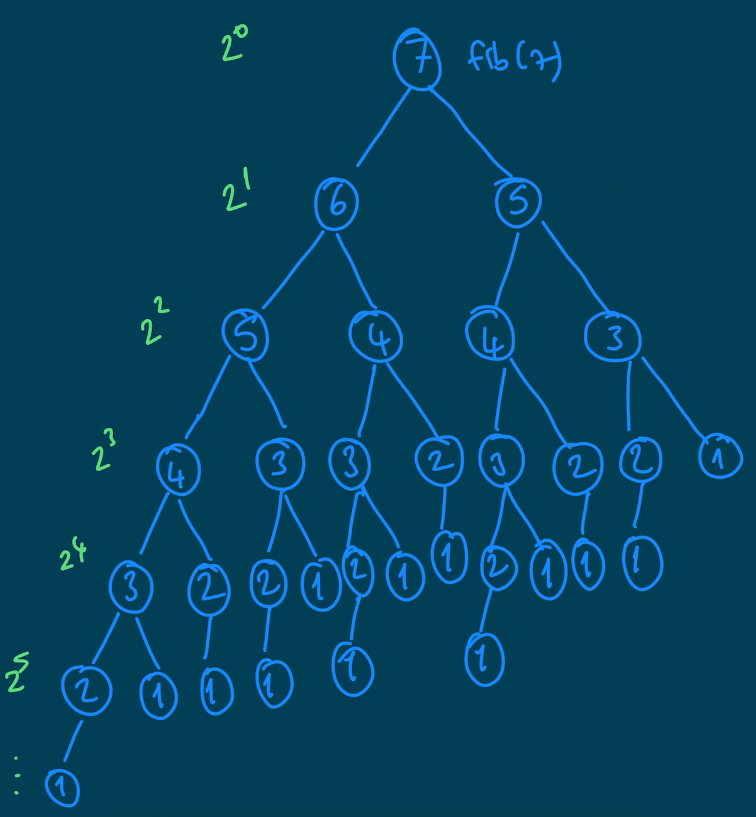
Bu metodun karmaşıklığını, recursive fonksiyonumuzun çağrılma sayısı olarak düşünebiliriz. Her adımda 2 farklı dala ayrıldığımız için sırasıyla; ilk adımda 1, ikinci adımda 2, üçüncü adımda 4 ... dala ayrılarak fonksiyonumuz kendini çağırmış. Örüntüyü görebildiniz mi? 2'nin üsleri şeklinde ilerleyen bir recursive çağrım olduğunu belirtiyor. Bu yüzden bu fonksiyonun zaman karmaşıklığı Q(2^n) olarak ifade edilir.

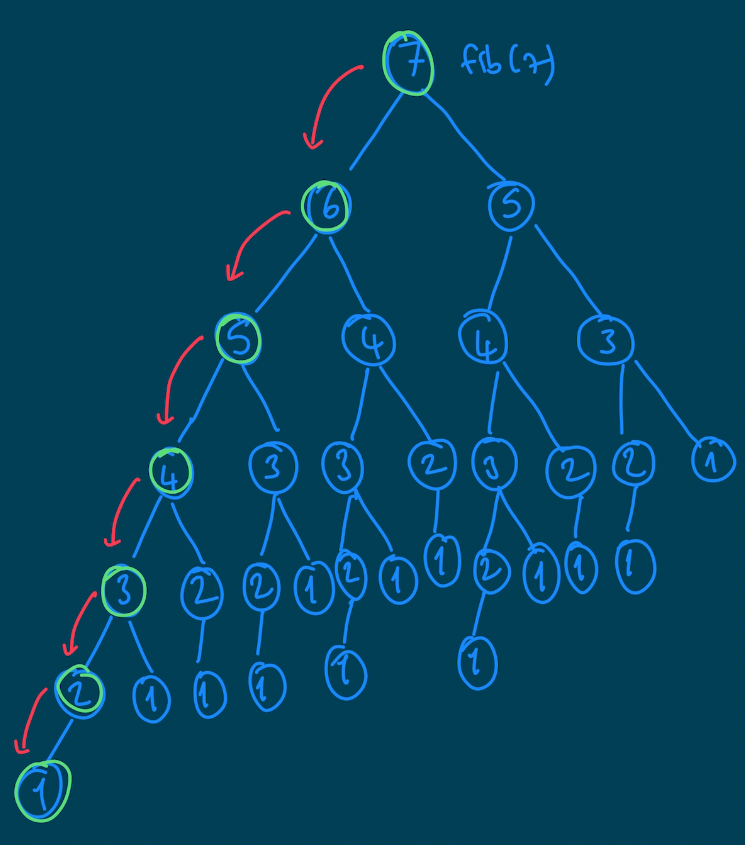
Alan karmaşıklığı ise bize fonksiyonumuzun hafızada (memory) işgal ettiği alan ile alakalıdır. Bizim fonksiyonumuzun call stack içerisinde kapladığı alanı düşünmemiz gerek. İlk bakışta aynı zaman karmaşıklığındaki gibi 2^n kadar hafıza tükettiğini düşünebilirsiniz. Ama bu size alan karmaşıklığını Q(2^n) yapmaz. Çünkü fonksiyonumuzun ilerleyişinde, yeşil işaretteki gibi hareket eder ve ilk adımda 7 kez fonksiyon çağırılır ve call stack'e eklenir. Ama fonksiyonun return değerini verdikten sonra, call stack'ten çıkarılır. Dolayısıyla daha fazla yer kaplamaz. O yüzden maksimum n kadar stack'te yer tüketiriz. Bu yüzden alan karmaşıklığımız Q(n) olur.

Gördüğünüz gibi alan karmaşıklığımız iyi ama zaman karmaşıklığımız parametremize bağlı üssel bir değer.  Bu yüzden iki metodla da karmaşıklığı azaltmaya çalışalım.

Memoization

İsmini "memo"(not) kelimesinden alır. Yukarıdaki ağaç yapısına bakarsak, birbirini tekrar eden örüntüler yakalayabiliyoruz. Mesela;

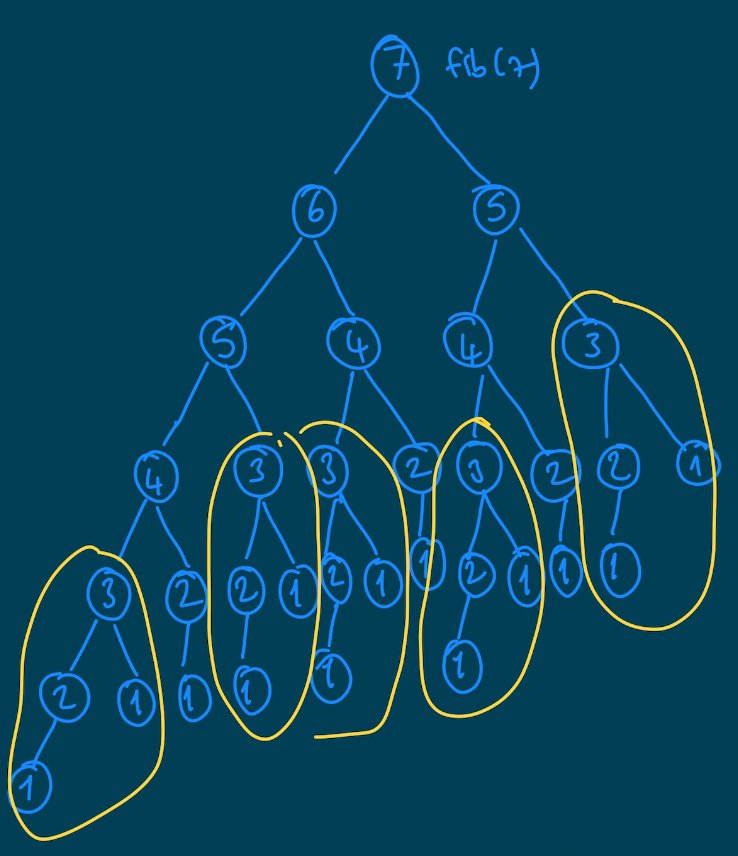
Gördüğünüz gibi bazı dallarda aynı değeri hesaplamak için tekrar ve tekrar fonksiyonumuz kendini çağırıyor. Eğer daha önceki hesapladığımız değeri bir yere kaydedersek, aynı değer için tekrar bir call yapmak zorunda kalmayız. Gelin yapalım.

const fib = (n, memo = {}) => {
  if (n in memo) return memo[n];
  if (n <= 2) return 1;

  memo[n] = fib(n-1, memo) + fib(n-2, memo);
  return memo[n];
};

console.log(fib(6)); 
console.log(fib(50)); // Çok hızlı şekilde hesaplanacak

Gördüğünüz gibi, fib fonksiyonumuza memo objesi tanımladık ve ilk değer olarak boş bir obje atadık. Return değerimizi, bu memo objesinde saklayarak, daha sonra aynı n değeri için tekrar gelindiğinde hesaplanmış değeri kullandık. Böylece fonksiyonumuz hızlandı. Peki zaman karmaşıklığı ne oldu?

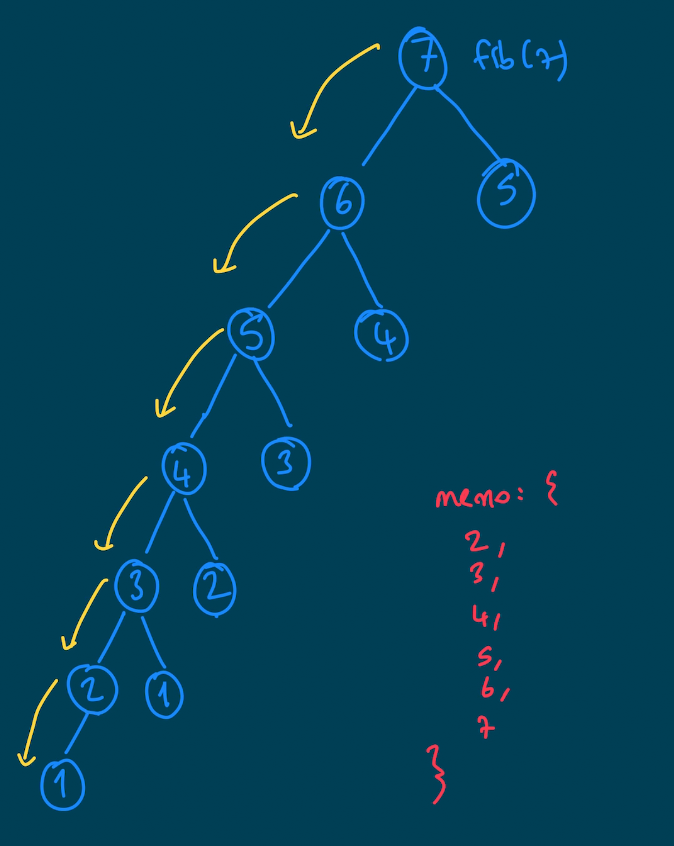
Sarı okları takip ederek fonksiyonumuz çalışır ve hesapladığı değerleri memoya kaydeder. Dolayısıyla dalların sağ tarafındakiler çoktan hesaplanmış olur. Bu yüzden 2*n kadar fonksiyonu çağrısı olur. Zaman karmaşıklığında değişken olmayan değerlerin bir önemi olmadığından, memoization çözümümüzle üssel karmaşıklığı Q(n)'e çekebildik. Baya havalı değil mi?

Tabulation

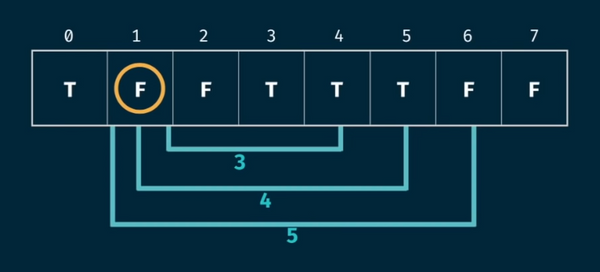
Bu yöntemde ise iteratif şekilde daha sonraki elemanları hesaplayarak gideceğiz. Fibonacci dizilimini düşünürsek, bir sonraki elemanın önceki 2 elemanın toplamı olduğunu biliyoruz. 6.elemanı bulmaya çalışırsak;

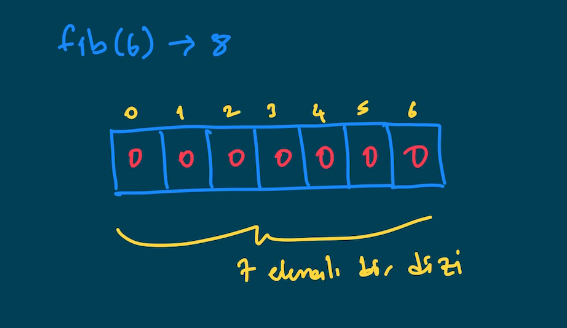
Öncelikle 7 (n+1) elemanlı bir dizi oluşturuyoruz. Çünkü 6.elemanı da 6. indiste göstermek istiyoruz. Fibonacci diziliminde bir toplama işlemi söz konusu olduğundan dizinin ilk değerlerini 0 atamak gayet mantıklı. Bu aşamadan sonra diğer elemanları hesaplamamız gerekiyor ama bize base değerler lazım. fib(1) = 1 olduğunu bildiğimize göre onu da tablo da ilklendirelim ve daha sonrasında diğer değerleri hesaplayalım.

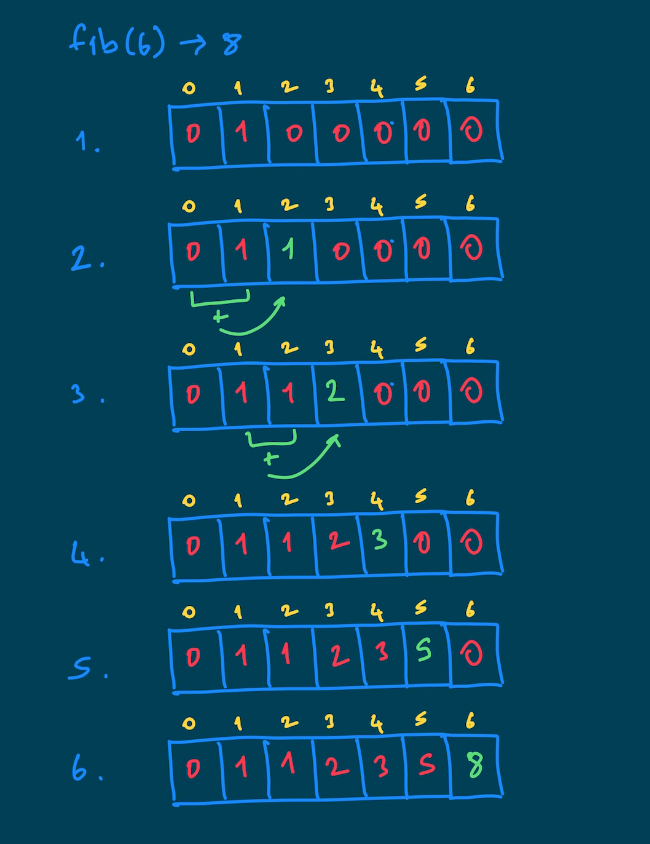
Gördüğünüz gibi adım adım bir sonraki elemanı hesaplayıp ve bu bilgiyi dizide saklayarak, 6.adımda aradığımız değere erişiyoruz. Şimdi bu işlemleri koda dökelim.

const fib = (n) => {
  
  // Bir array oluşturalım ve tüm elemanları 0 yapalım.
  const arr = Array(n+1).fill(0);
    
  // Sekansın 1.elemanının 1 olduğunu biliyoruz.
  arr[1] = 1;

  // Sırayla diğer elemanları hesaplayalım
  for (let i = 2; i <= n; i++) {
     arr[i] = arr[i-1] + arr[i-2];
  }

  // Dizinin n. elemanı aradığımız değer
  return arr[n];
}

Bu sefer de tabulation yöntemi kullanarak fonksiyonumuzu yazdık. Baktığımızda hafızada sadece n elemanlı bir dizi tutuyoruz. Bundan dolayı alan karmaşıklığımız Q(n). Burada karmaşıklığı etkileyen ve tekrar eden işlem for döngüsü ve n kere (n-2 kere ama n'in yanında 2'yi göz ardı edebiliriz) atama işlemi oluyor. Bu da her bir n değeri için n kadar işlem yapılıyor anlamına geliyor. Dolayısıyla zaman karmaşıklığımız da Q(n) oluyor.

Aslında baktığınızda tabulation yöntemiyle de bir ağaç yapısı oluşturuyoruz ve bunu bir dizi kullanarak yapıyoruz.

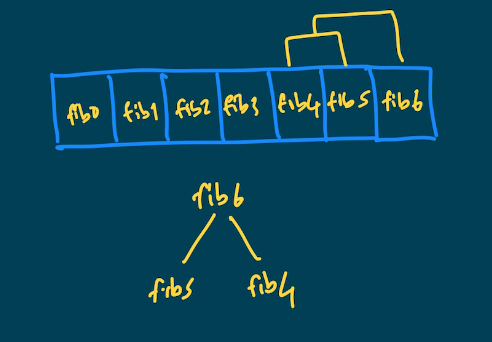
Bu yazımla beraber dinamik programlama yöntemleri olan memoization ve tabulation'a bir giriş yapmış olduk. Bu yöntemi farklı problemlerde de kullanarak pekiştireceğiz. Bir sonraki yazımda canSum problemi üzerinden seriye devam edeceğiz.